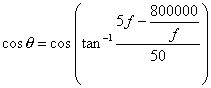Saadat's Website Pspice EE 230

PSpice Examples for EE-230
Hadi Saadat

Download PSPICE Schematic files for EE-230. To view the Pspice examples you need to download the OrCAD Viewer Free Download. To run the examples, students can download the complete Free OrCAD Software for Students.

Example 1	Example 2	Example 3	Example 4	Example 5
Example 6	Example 7	Example 8	Example 9	Example 10
Example 11	Example 12	Example 13	Example 14

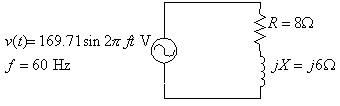
Part 1 AC Power and Three-phase Circuits

Example 1

For the circuit shown, use PSpice and Probe to graph the instantaneous voltage, current and power over one cycle.

The initial current in the inductor is given to be -10.1826 A. The reactor inductance is

. The PSpice Schematic is as shown.

Select Transient analysis, set the final time to 16.6667 ms, and the Step Ceiling to 0.01 ms. In Probe plot the instantaneous voltage V(1), and from Plot add Y-axis and the trace for current I(R1). Repeat to add the Y-axis and the trace for the instantaneous power p (t), (in probe for trace expression type V(1)*I(R1)).

The real power can be expressed as , and the reactive power as

Select the power axis and add the traces with Trace Expressions as 8*MAX(I(R1))*MAX(I(R1))/2, and 6*MAX(I(R1))*MAX(I(R1))/2 to display P and Q.

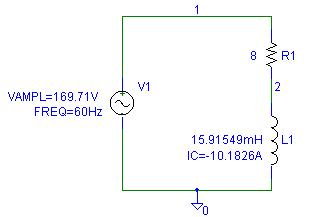
* Schematics Netlist *

L_L1 2 0 15.91549mH IC=-10.1826A

R_R1 1 2 8

V_V1 1 0 +SIN 0 169.71V 60Hz 0 0 0

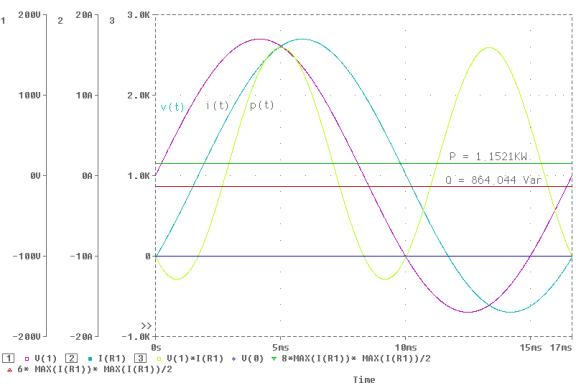
The result is shown in the next page.

Top of Page

Example 2

For the circuit shown, use PSpice and Probe to graph the real and reactive powers delivered to the circuit as a function of frequency. Use the AC analysis to sweep the source frequency from 300 Hz to 500 Hz in steps of 1 Hz and Probe to obtain one graph showing real and reactive power supplied by the source and another graph showing power factor as a function of frequency. Determine the source frequency for unity power factor.

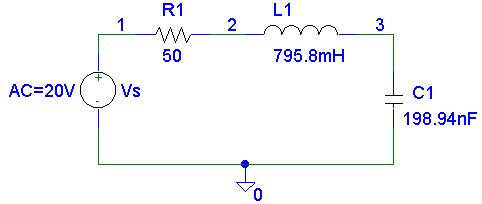
* Schematics Netlist *

R_R1 1 2 50

V_Vs 1 0 AC 20V

L_L1 2 3 795.8mH IC=0

C_C1 3 0 198.94nF IC=0

The circuit impedance is

The real power is

and the reactive power is

The power factor is

In probe, select Plot control and Add Plot to create two graphs on the screen. Select X-axis and set the range to change the frequency axis scale to 350 450 Hz. Using Add Trace plot P and Q with the trace expressions given by (2) and (3).

Use Plot Control, select plot and down key to switch to the lower graph and using Add Trace add the power factor with the Trace Expression as given by (4). Using the cursor command you can move along the plot with the right or left arrows. The co-ordinates at which the cursor is located are displayed on the lower right hand of the screen. You can select between different plots by holding down the control key while pressing the right or left arrow keys. Using the Label command you can add text, lines and arrows to the plot. 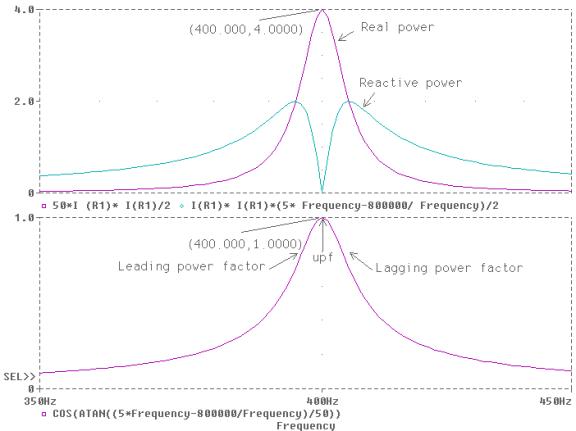The plot produced on the probe is shown below. From the plots we see that the circuit changes from capacitive to inductive at the series resonance frequency where reactive power is zero.

At unity power factor frequency, f = 400 Hz, P = 4 W

Top of Page

Example 3

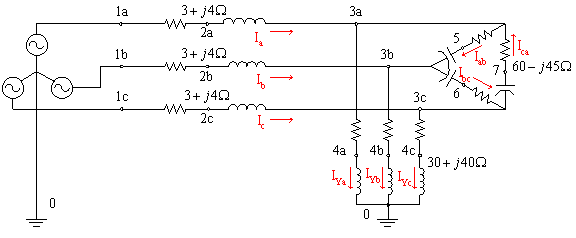
A 3-phase line has an impedance of 3 + j4 W. The line feeds two balanced three-phase loads that are connected in parallel. The first load is Y-connected and has an impedance of 30 + j40 W/phase. The second load is delta connected and has an impedance of 60 - j45 W/phase. The line is energized at the sending-end from a 3-phase balanced supply of line to neutral voltage (rms), 60 Hz. Determine

(a) Current in the line for each phase.

(b) Current in each phase of the Y-connected loads.

The line inductance per phase is

The Y-connected load inductance per phase is

The D-connected load capacitance per phase is

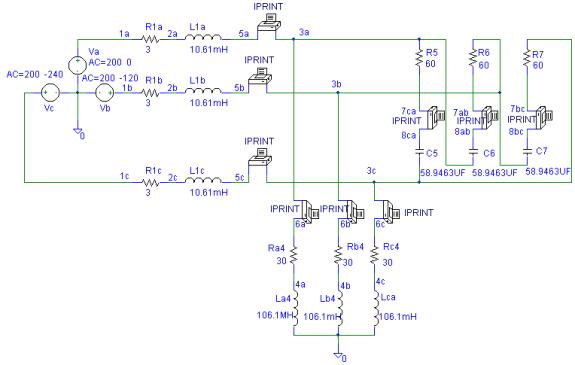
The Schematic and the Netlist are shown in the following pages. The output files contain the following values for the magnitude and phase angle of currents.

FREQ IM(V_PRINT1) IP(V_PRINT1)

6.000E+01 8.000E+00 -6.388E-05

FREQ IM(V_PRINT2) IP(V_PRINT2)

6.000E+01 8.000E+00 -1.200E+02

FREQ IM(V_PRINT3) IP(V_PRINT3)

6.000E+01 8.000E+00 1.200E+02

FREQ IM(V_PRINT7) IP(V_PRINT7)

6.000E+01 3.578E+00 -6.343E+01

FREQ IM(V_PRINT8) IP(V_PRINT8)

6.000E+01 3.578E+00 1.766E+02

FREQ IM(V_PRINT9) IP(V_PRINT9)

6.000E+01 3.578E+00 5.657E+01

FREQ IM(V_PRINT10) IP(V_PRINT10)

6.000E+01 4.131E+00 1.766E+02

FREQ IM(V_PRINT11) IP(V_PRINT11)

6.000E+01 4.131E+00 5.657E+01

FREQ IM(V_PRINT12) IP(V_PRINT12)

6.000E+01 4.131E+00 -6.343E+01

From the above results the currents are:

(a) The line currents

, , and

(b) Currents in the Y-connected loads are:

, , and

* Schematics Netlist *

R_R1a 1a 2a 3

R_R1b 1b 2b 3

L_L1a 2a 5a 10.61mH

L_L1b 2b 5b 10.61mH

L_La4 4a 0 106.1MH

L_Lb4 4b 0 106.1mH

L_Lca 4c 0 106.1mH

R_Ra4 6a 4a 30

R_Rb4 6b 4b 30

R_Rc4 6c 4c 30

C_C5 8ca 3c 58.9463UF

R_R7 3c 7bc 60

L_L1c 2c 5c 10.61mH

R_R1c 1c 2c 3

V_Vc 1c 0 AC 200 -240

V_Va 1a 0 AC 200 0

V_Vb 1b 0 AC 200 -120

C_C6 8ab 3a 58.9463UF

R_R5 3a 7ca 60

C_C7 8bc 3b 58.9463UF

R_R6 3b 7ab 60

V_PRINT9 3c 6c 0V

.PRINT AC

+ IM(V_PRINT9)

+ IP(V_PRINT9)

V_PRINT1 5a 3a 0V

.PRINT AC

+ IM(V_PRINT1)

+ IP(V_PRINT1)

V_PRINT2 5b 3b 0V

.PRINT AC

+ IM(V_PRINT2)

+ IP(V_PRINT2)

V_PRINT3 5c 3c 0V

.PRINT AC

+ IM(V_PRINT3)

+ IP(V_PRINT3)

V_PRINT7 3a 6a 0V

.PRINT AC IM(V_PRINT7)

V_PRINT8 3b 6b 0V

.PRINT AC

+ IM(V_PRINT8)

V_PRINT10 8ca 7ca 0V

.PRINT AC

+ IM(V_PRINT10)

+ IP(V_PRINT10)

V_PRINT11 8ab 7ab 0V

.PRINT AC

+ IM(V_PRINT11)

+ IP(V_PRINT11)

V_PRINT12 8bc 7bc 0V

.PRINT AC

+ IM(V_PRINT12)

+ IP(V_PRINT12)

Top of Page

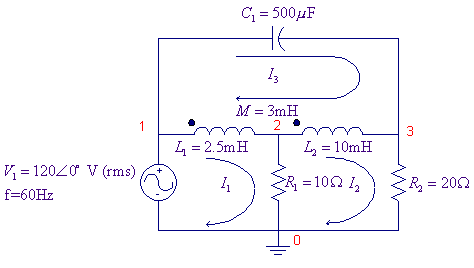
Mutually Coupled Circuits

Example 4

Determine the magnitudes and phase angles of mesh currents in the coupled circuit shown.

PSpice uses the coupling coefficient to describe the coupled coils, thus we find K from

The “dot” convention for the coupling is related to the direction in which the inductors are connected. The dot is always next to the first pin to be netlisted. When the inductor symbol, L, is taken from the part library and is placed without rotation, the “dotted” pin is the left one. Edit/Rotate (<Ctrl R>) rotates the inductor +90deg, which makes this pin the one at the bottom. The dotted terminal is always referred to the first node of the inductor in the Netlist. So always examine the net list and if the left node is not the dotted side, rotate the inductor in the schematic until the desired dotted node is the first entry in the Netlist. The part K_linear can be used to specify the mutual coupling between two or more inductors. The parameters to be specified are L1, L2, … up to L6, whose values must be set to the inductors symbols. The coupling value is the coefficient of mutual coupling, which must be specified between zero and 1. 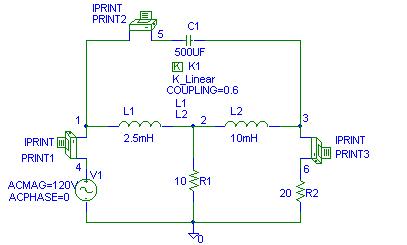The PSpice schematics is as shown.

Three IPRINT symbols are inserted in series in each loop to write the currents in the output file. In the text box for each IPRINT set AC, MAG and PHASE to YES. From the analysis menu select the Probe Setup, and disable the Probe. Enable the AC Analysis, select Linear, and set the Total pts to 1, Start and End Frequencies to 60. Run PSpice (Analysis, Simulate). The Schematics Netlist is as follows

L_L1 1 2 2.5mH

L_L2 2 3 10mH

C_C1 5 3 500UF

R_R1 2 0 10

V_PRINT3 3 6 0V

.PRINT AC

+ IM(V_PRINT3)

+ IP(V_PRINT3)

V_V1 4 0 DC 0V AC 120V 0

R_R2 6 0 20

Kn_K1 L_L1 L_L2 0.6

V_PRINT2 1 5 0V

.PRINT AC

+ IM(V_PRINT2)

+ IP(V_PRINT2)

V_PRINT1 4 1 0V

.PRINT AC

+ IM(V_PRINT1)

+ IP(V_PRINT1)

The output file contains the following values for the magnitude and angles of the currents

FREQ IM(V_PRINT1) IP(V_PRINT1)

6.000E+01 1.164E+01 3.133E+01

FREQ IM(V_PRINT2) IP(V_PRINT2)

6.000E+01 2.438E+01 5.200E+01

FREQ IM(V_PRINT3) IP(V_PRINT3)

6.000E+01 4.083E+00 7.719E+01

From the above results, the mesh currents are:

Top of Page

Example 5

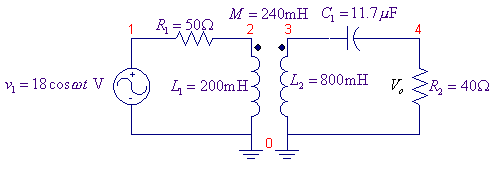
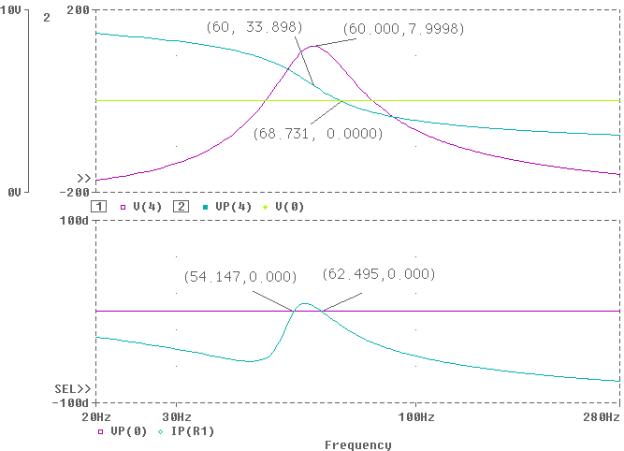
For the circuit shown, use PSpice and Probe to graph the magnitude and phase angle of the output voltage V_o, i.e., V(4) as a function of frequency. Use the AC analysis to sweep the source frequency linearly from 20 HZ to 280HZ in steps of 1HZ. Determine the frequency at which the amplitude of the output voltage V_o is a maximum; find the phase angle at this frequency. Also, find the frequency at which the impedance seen by the source is purely resistive.

First we calculate the coefficient of coupling

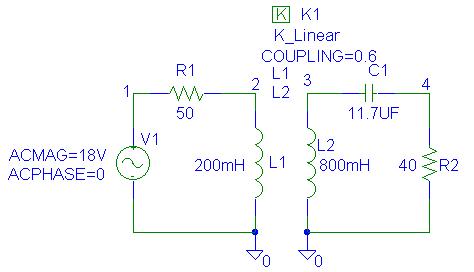
The PSpice Schematic is as shown.

The Schematics Netlist is as follows:

Kn_K1 L_L1 L_L2 0.6

R_R1 1 2 50

R_R2 4 0 40

V_V1 1 0 DC 0V AC 18V 0

C_C1 3 4 11.7UF

L_L1 2 0 200mH

L_L2 3 0 800mH

Since the dotted terminal is always the first pin in the Netlist, L1 and L2 are rotated three times such that their corresponding nodes are entered as 2 0, and 3 0 respectively.

In probe, Add Plot from the Plot menu to create two graphs on the screen. Using Add from the Trace menu plot V(4). From Plot use Add Y axis to create a new Y-axis, and add the trace for voltage phase angle VP(4). Select Cursor from the Tools menu, select the Display and use Peak to find the peak voltage. Use Label from the Tools menu and Mark the values at the peak position. Switch the Cursor to phase angle plot and Mark the values at the frequency corresponding to the peak value. Switch to the lower graph and use Trace to add the input voltage and the input current phase angles VP(1) and IP(R1). Use Cursor and Mark to get the frequencies at 0. The Probe result is as shown. From the graph the maximum output voltage is V = at 60 Hz. From the lower graph, the input impedance is purely resistive at frequencies 54.147Hz, and 62.495 Hz.

Top of Page

Example 6

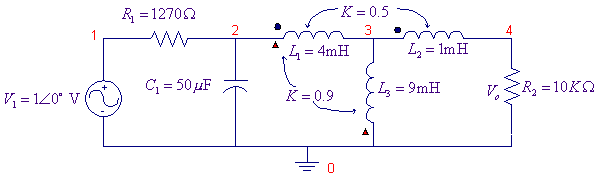
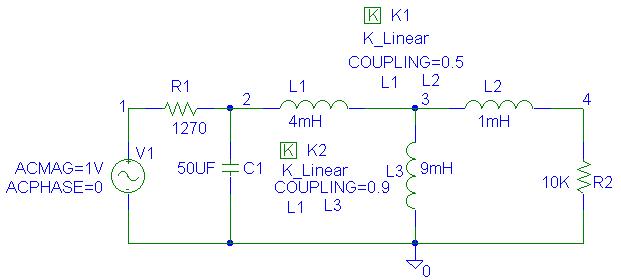
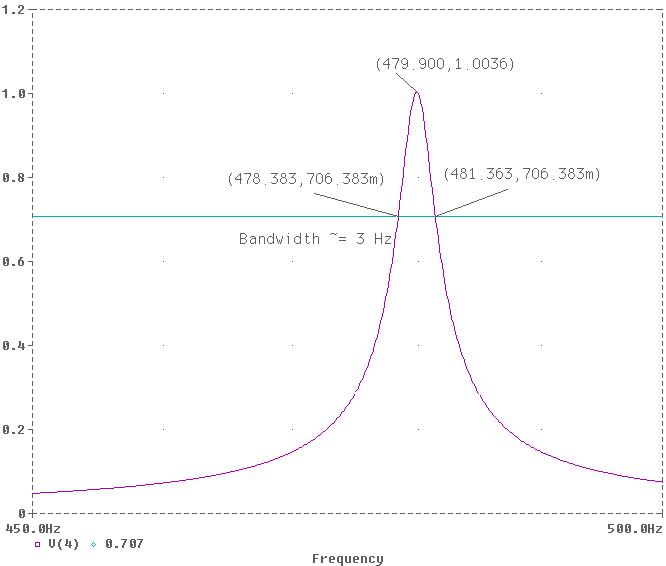
For the circuit shown, L₁ and L₂ are mutually coupled with a coupling coefficient of K = 0.5. Also, L₁ and L₃ are mutually coupled with a coupling coefficient of K = 0.9. Use PSpice and Probe to graph the magnitude of the output voltage V_o as a function of frequency. Use the AC analysis to sweep the source frequency linearly from 450HZ to 500HZ in steps of 0.1HZ. Determine the frequency at which the amplitude of the output voltage V_o is a maximum. If bandwidth is the frequency range within 0.707 of the peak value, find the bandwidth.

Two K_linear parts are used to specify the mutual coupling between L₁, L₂, and L₁, L₃. Since the dotted terminal is always the first pin in the Netlist, L3 is rotated once such that the corresponding nodes for L1 and L3 are entered as 2 3, and 0 3 respectively.

The PSpice Schematic is as shown.

The Schematics Netlist is

L_L2 3 4 1mH

V_V1 1 0 DC 0V AC 1V 0

L_L1 2 3 4mH

R_R1 1 2 1270

C_C1 2 0 50UF

Kn_K1 L_L1 L_L2 0.5

R_R2 4 0 10K

Kn_K2 L_L1 L_L3 0.9

L_L3 0 3 9mH

Use Add from the Trace menu to plot V(4). From plot use the X_Axis Settings and set the range from 450 Hz to 500 Hz. Select Cursor from the Tools menu, check the Display and use Peak to find the peak voltage. Use Label from the Tools menu and Mark the values at the peak position. Add a trace at 0.707 of the peak value. Use Cursor to Mark the corner frequencies at the intersection with the 0.707 line. Determine the bandwidth and Mark it on the graph. The probe result is shown. From the graph the maximum output voltage is at 479.9Hz. The corner frequencies are f₁ = 478.383Hz, f₂ = 481.363Hz and the bandwidth is approximately 3.0 Hz.

Top of Page

Example 7

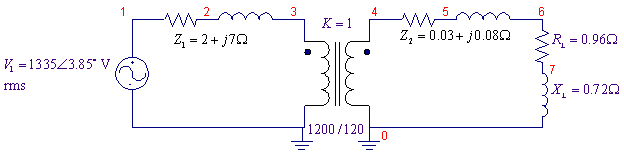
A 1200/120 V single-phase transformer has the following primary and secondary winding impedances, HV winding: , LV winding: . The voltage at the primary side of the transformer is (rms), 60 HZ. Transformer is supplying a load of at its low voltage terminal. Determine the load voltage and current.

From the given reactances at 60 HZ, the inductances are given by

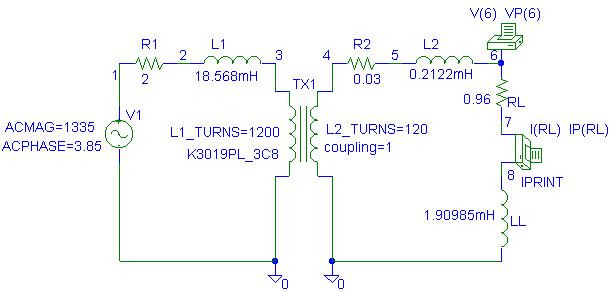
We can use K3019PL non-linear core to model the transformer, to model the ideal transformer the coupling coefficient is set to 1. The L1_Turns and L2_Turns values are set to 1200 and 120 respectively. The PSpice Schematic is as shown.

The Schematics Netlist is

R_R2 4 5 0.03

L_L2 5 6 0.2122mH

R_R1 1 2 2

R_RL 6 7 0.96

L1_TX1 3 0 1200

L2_TX1 4 0 120

K_TX1 L1_TX1 L2_TX1 1 K3019PL_3C8

L_L1 2 3 18.568mH

L_LL 8 0 1.90985mH

V_V1 1 0 DC 0V AC 1335 3.85

.PRINT AC

+ VM([6])

+ VP([6])

V_PRINT2 7 8 0V

.PRINT AC

+ IM(V_PRINT2)

+ IP(V_PRINT2)

Double-click on the VPRINT1 symbol. Select 'SIMULATIONONLY=' and for value type V(6) VP(6). In the text box for VPRINT1 set AC, MAG and PHASE to YES. Also in the text box for IPRINT set AC, MAG and PHASE to YES. From the analysis menu select the Probe Setup and disable the Probe. Enable the AC Analysis, select Linear, and set the Total pts to 1, Start and End Frequencies to 60. Run PSpice (Analysis, Simulate). The output file contains the following values for the magnitude and phase angle of currents.

FREQ VM(6) VP(6)

6.000E+01 1.200E+02 3.730E-04

FREQ IM(V_PRINT2) IP(V_PRINT2)

6.000E+01 1.000E+02 -3.687E+01

That is,

Example 8

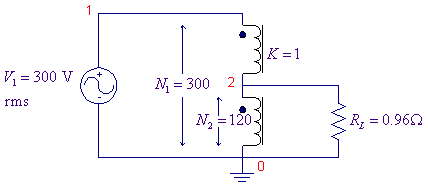
A 300/120V ideal autotransformer is supplying a load from a 300 V source. Find the secondary load current.

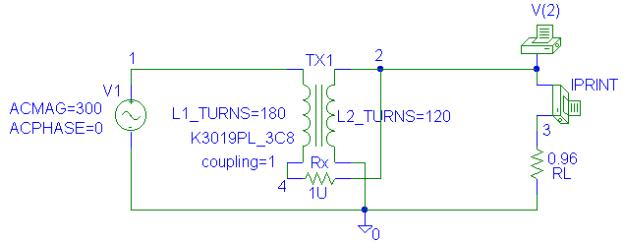
We can use K3019PL non-linear core to model the transformer, to model the ideal transformer the coupling coefficient is set to 1. For L1_Turns, we use , and L2_Turns 120. PSpice will not allow a loop of all inductor and voltage source. To avoid this in the primary loop a negligible resistance ( ) is added. The PSpice Schematic is as shown.

The Schematics Netlist is

L1_TX1 1 4 180

L2_TX1 2 0 120

K_TX1 L1_TX1 L2_TX1 1 K3019PL_3C8

V_V1 1 0 DC 0V AC 300 0

R_RL 3 0 0.96

.PRINT AC

+ VM([2])

V_PRINT2 2 3 0V

.PRINT AC

+ IM(V_PRINT2)

R_Rx 4 2 1U

Double-click on the VPRINT1 symbol. Select 'SIMULATIONONLY=' and for value type V(2). In the text box for VPRINT1 set AC and MAG to YES. Also in the text box for IPRINT set AC and MAG to YES. From the analysis menu select the Probe Setup and disable the Probe. Enable the AC Analysis, select Linear, and set the Total pts to 1, Start and End Frequencies to 60. Run PSpice (Analysis, Simulate). The output file contains the following values:

FREQ VM(2)

6.000E+01 1.200E+02

FREQ IM(V_PRINT2)

6.000E+01 1.250E+02

That is, V_L = 120 V, and I_L = 125 A.

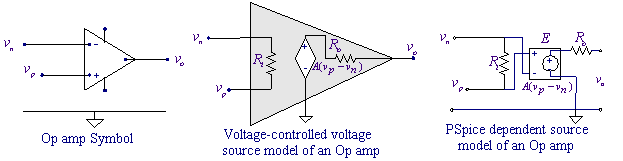
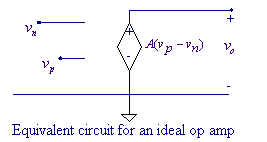
Operational Amplifiers

The operational amplifier (called op amp) is an electronic device that has become a versatile network element. The main characteristics of an op amp are very high input resistance, very low output resistance, and very high gain (to the order of 10⁵). By focusing on the terminal behavior of an op amp, one can appreciate its use as a network element without knowledge of its internal behavior. The PSpice evaluation version has only one op amp (UA741), and only two of these can be used before reaching the component limits. If you have a circuit with a large number of op amps, you will be forced to use ideal op amps in the evaluation version. The op amp may be modeled as a linear amplifier to simplify the design and analysis of op amp circuits. A voltage-controlled voltage source can be used to model an op amp in the linear range with reasonable accuracy as shown in the Figure below.

is a very high value and has a very small value. For the UA741 op amp, the typical value for A, R_i, and R_o are 10⁵, 2 MEGW, and 75W, respectively. For ideal op amp R_i = ¥, and R_o = 0 and A must be given a very high number. A gain of A=1E10 works well and gives ideal op amp answers. PSpice can represent the infinite input resistance by an open-circuit and zero output resistance by a short circuit, and a very large number can approximate the infinite gain. A gain of 10¹⁰ works well, and gives ideal op amp answers.

Top of Pag

Example 9 (EE230.Ex9.sch)

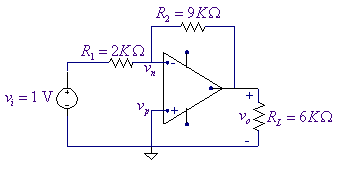
For the circuit shown below assume an ideal op amp and use Spice to calculate the voltage gain

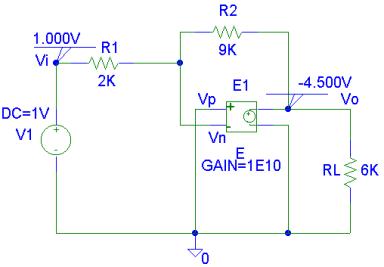
A voltage-controlled voltage source (Part E) is used. The voltage gain is set to 1E10. The input and output node voltages are viewed using the VIEWPOINT part. The PSpice schematic containing the simulation result is as shown below.

Schematics Netlist is

V_V1 Vi 0 DC 1V

E_E Vo 0 0 Vn 1E10

R_R2 Vn Vo 9K

R_RL Vo 0 6K

R_R1 Vi Vn 2K

Thus the voltage gain is -4.5.

Top of Pag

Example 10 (EE230Ex10.sch)

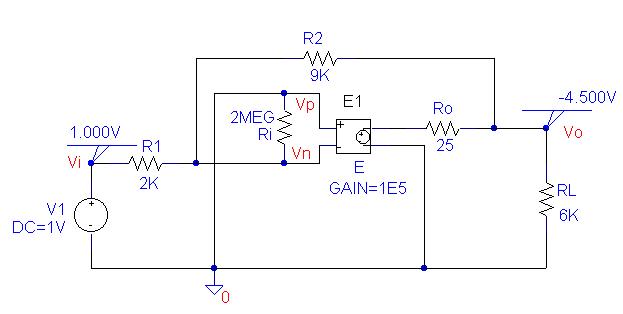
For Example 9 use a more realistic model with the following parameters

The PSpice schematic containing the simulation result is as shown below.

Schematics Netlist is

R_RL Vo 0 6K

V_V1 Vi 0 DC 1V

R_R1 Vi Vn 2K

R_Ri Vn 0 2MEG

E_E $N_0001 0 0 Vn 1E5

R_R2 Vn Vo 9K

R_Ro $N_0001 Vo 25

Thus the voltage gain is = -4.5 V approximately the same as the ideal op amp model.

Top of Page

Example 11 (EE230Ex11.sch)

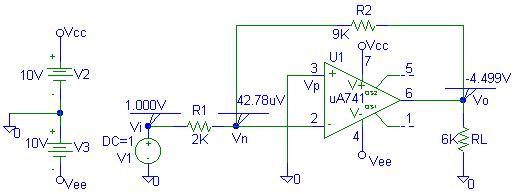
For Example 10 use a UA741 op amp. The op amp positive power supply V_cc = 10 V, and the negative power supply is V_ee = 10 V. Two parts named BUBBLE are connected to the supply nodes. Click on each BUBBLE to name these terminals V_cc and V_ee. Two DC supply of 10 V with BUBBLES named V_cc, and V_ee are made as shown to provide the necessary voltages for terminal 7 and 4 of the op amp. The PSpice schematic containing the simulation result is as shown below.

Schematics Netlist is

R_R1 Vi Vn 2K

R_R2 Vn Vo 9K

V_V3 0 Vee 10V

V_V2 Vcc 0 10V

X_U1 0 Vn Vcc Vee Vo uA741

V_V1 Vi 0 DC 1

R_RL Vo 0 6K

Thus the voltage gain is = -4.499 compared to -4.5 obtained with the ideal op amp model.

Top of Pag

Example 12 (EE230Es12.sch)

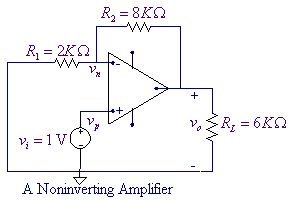
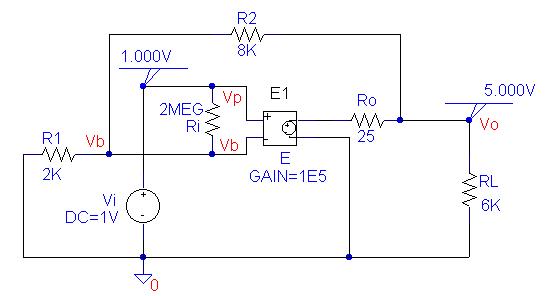
Determine the voltage gain in the noninverting amplifier circuit shown. The amplifier parameters are

The PSpice schematic containing the simulation result is as shown below.

The Schematics Netlist is

V_Vi Vp 0 DC 1V

R_Ri Vb Vp 2MEG

R_R1 0 Vb 2K

E_E $N_0001 0 Vp Vb 1E5

R_R2 Vb Vo 8K

R_Ro $N_0001 Vo 25

R_RL Vo 0 6K

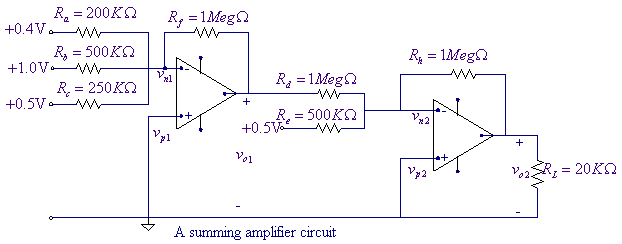
Thus, the voltage gain is , the same as the ideal op amp voltage gain which is

Top of Page

Example 13 (EE230Ex13.sch, EE230Ex13b.sch)

In the circuit shown below, determine

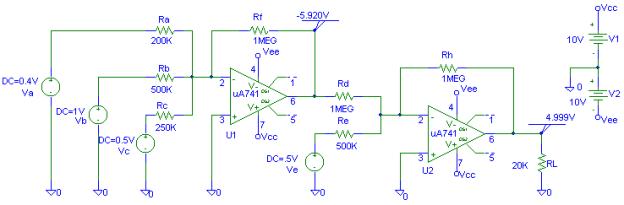
(a) Use two UA741 op amps. The op amp positive power supply V_cc = 10 V, and the negative power supply is V_ee = 10 V.

The PSpice schematic containing the simulation result is as shown below.

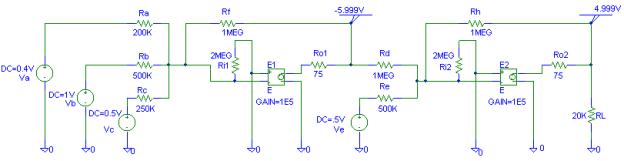
(b) Use to voltage-controlled voltage source to model the op amps. The parameters of each op amp are

The PSpice schematic containing the simulation result is as shown below. (EE230Ex13b.sch)

Top of Page

Example 14

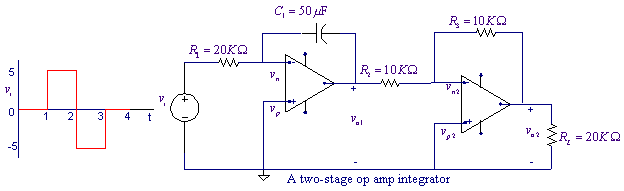
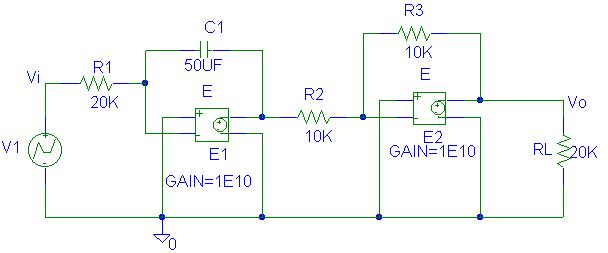
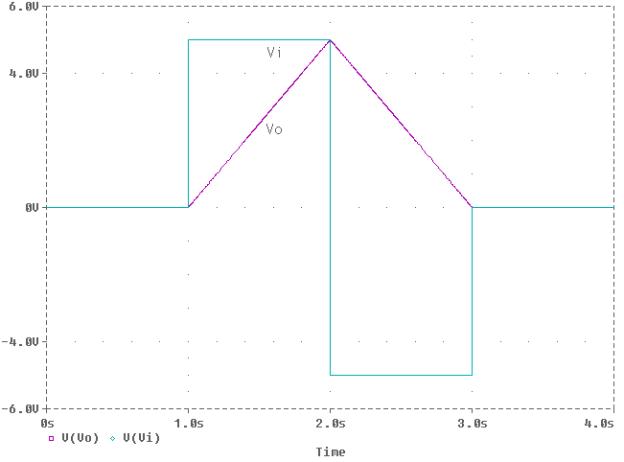
The source voltage in the circuit shown uses the PSpice VPWL function to generate a waveform that is zero from 0 to 1 second, jumps to +5 at t = 1 second, jump down to -5 at t = 2 second, jumps back to zero at t = 3 seconds and remains at zero. The first op amp is an inverting integrator. The second op amp is a unity gain inverter. The overall circuit is a noninverting integrator with a gain of .

The output is the integral of the input as shown below. Appling KCL at the inverting node, we get

For an ideal op amp , and , thus we have

Since the second op amp is a unity gain inverter, we have

Substituting for and , , and the output is the integral of the input,

Two voltage-controlled voltage sources with gains of 10¹⁰ are used to represent the ideal op amps. The PSpice schematic is as shown.

The Transient analysis is used to simulate the circuit over a period of 4 seconds. The Probe is used and the graph containing and plots is shown in the next page.

Top of Page